When we generate data such as this...

• We assume that the predictors are not correlated with each other (they are generated independently)

set.seed(12345); ns <- 1000
x1 <- rnorm(ns); x2 <- rnorm(ns); err <- rnorm(ns)
y <- 1 + .5 * x1 + .5 + x2 + err
cor(x1, x2)

[1] 0.03877533

• This is fine but then the expected correlation of x1 and x2 = 0
• Many, times this may not be realistic
• We may want to generate correlated data (e.g, to simulate multicollinearity)

Generating correlated normal variables (from a multivariate normal distribution): bivariate case

If only two variables, can use the formula: $$y_1=\rho x_1+\sqrt{(1-{\rho }^2)}{x}_2$$

• where $\rho$ is the desired correlation (e.g., .5)
• x1 and x2 are two independent variables

x1 <- rnorm(10000); x2 <- rnorm(10000); rho <- .5
y <-  rho * x1 + (sqrt(1 - rho^2) * x2)
cor(x1, y)

[1] 0.5106397

Generating correlated normal variables (from a multivariate normal distribution): multivariate case

# set.seed(123)
# x1 <- rnorm(1000)
# x2 <- rnorm(1000)
# x3 <- rnorm(1000)
## target correlation matrix:: what we want
tarcor <- matrix(c(1, .3, .5,
                   .3, 1, .2,
                   .5, .2, 1), byrow = T, ncol = 3)
tarcor

     [,1] [,2] [,3]
[1,]  1.0  0.3  0.5
[2,]  0.3  1.0  0.2
[3,]  0.5  0.2  1.0

Steps: Methods developed by Kaiser and Dickman (1962)

$${\hat{Z}}_{(k\times N)}=F_{(k\times k)}{X}_{(k\times N)}$$

eig <- eigen(tarcor) #has eigenvalues and eigenvectors
ev <- eig$values
evec <- eig$vectors
n <- 10000
p <- 3
# shortcut for just creating 3 random vars
X <- matrix(rnorm(n * p), ncol = p)
zhat <-  t(evec %*% diag(sqrt(ev)) %*% t(X))
cor(zhat)

          [,1]      [,2]      [,3]
[1,] 1.0000000 0.2907589 0.4978043
[2,] 0.2907589 1.0000000 0.1819259
[3,] 0.4978043 0.1819259 1.0000000

tarcor #target correlation for comparison

     [,1] [,2] [,3]
[1,]  1.0  0.3  0.5
[2,]  0.3  1.0  0.2
[3,]  0.5  0.2  1.0

NOTE: The original correlation matrix can be recreated using the eigenvalues and the eigenvectors

The original matrix can be decomposed into these matrices...

$$\Sigma =\Lambda \varphi {\Lambda }^{\prime }$$ where: $\Lambda$ = k $\times$ k matrix of eigenvectors and $\varphi$ = k $\times$ k diagonal matrix with eigenvalues on the diagonal.

evec %*% diag(ev) %*% t(evec) #from previous slide

     [,1] [,2] [,3]
[1,]  1.0  0.3  0.5
[2,]  0.3  1.0  0.2
[3,]  0.5  0.2  1.0

tarcor

     [,1] [,2] [,3]
[1,]  1.0  0.3  0.5
[2,]  0.3  1.0  0.2
[3,]  0.5  0.2  1.0

To get the transformation matrix : Same as the principal components (signs might differ)

$F=\Lambda \sqrt{\varphi }$

evec %*% diag(sqrt(ev)) #transformation matrix

          [,1]       [,2]       [,3]
[1,] 0.8390075  0.1745109  0.5153759
[2,] 0.5986054 -0.7913170 -0.1244547
[3,] 0.7884457  0.4150833 -0.4539374

## these are also the factor loadings from a PCA with no rotation 
## where the number of components = number of variables

psych::principal(tarcor, rotate = 'none', nfactors = 3)

Principal Components Analysis
Call: psych::principal(r = tarcor, nfactors = 3, rotate = "none")
Standardized loadings (pattern matrix) based upon correlation matrix
   PC1   PC2   PC3 h2       u2 com
1 0.84 -0.17 -0.52  1 -4.4e-16 1.8
2 0.60  0.79  0.12  1 -4.4e-16 1.9
3 0.79 -0.42  0.45  1  0.0e+00 2.2
                       PC1  PC2  PC3
SS loadings           1.68 0.83 0.49
Proportion Var        0.56 0.28 0.16
Cumulative Var        0.56 0.84 1.00
Proportion Explained  0.56 0.28 0.16
Cumulative Proportion 0.56 0.84 1.00
Mean item complexity =  2
Test of the hypothesis that 3 components are sufficient.
The root mean square of the residuals (RMSR) is  0 
Fit based upon off diagonal values = 1

Can do this with a variance/covariance matrix $\Sigma$:

tarcov <- matrix(c(36, -5.1, 1.8,
                   -5.1, .96, -.34,
                   1.8, -.34, .25), byrow = T, ncol = 3)
tarcov

     [,1]  [,2]  [,3]
[1,] 36.0 -5.10  1.80
[2,] -5.1  0.96 -0.34
[3,]  1.8 -0.34  0.25

eig2 <- eigen(tarcov) #has eigenvalues and eigenvectors
ev <- eig2$values
evec <- eig2$vectors
n <- 10000
p <- 3
# shortcut for just creating 3 random vars; could have just 
# generated x1, x2, x3; variances have to be the same!
X <- matrix(rnorm(n * p), ncol = p)
zhat <-  t(evec %*% diag(sqrt(ev)) %*% t(X))
#head(zhat, n = 4)
cov(zhat)

          [,1]       [,2]       [,3]
[1,] 36.454557 -5.1790291  1.8071540
[2,] -5.179029  0.9723781 -0.3392217
[3,]  1.807154 -0.3392217  0.2460346

Now that you know how to do this manually, much quicker way- MASS::mvrnorm

library(MASS) # built in with R; NOTE: has a `select` function 
# which may conflict with dplyr::select

Simulate from a Multivariate Normal Distribution Description Produces one or more samples from the specified multivariate normal distribution.

Usage: mvrnorm(n = 1, mu, Sigma, tol = 1e-6, empirical = FALSE, EISPACK = FALSE)

Using our last example...

Need to specify the means $\mu$ as well.

tarcov

     [,1]  [,2]  [,3]
[1,] 36.0 -5.10  1.80
[2,] -5.1  0.96 -0.34
[3,]  1.8 -0.34  0.25

zhat2 <- mvrnorm(n = 1000, mu = c(20, 3.2, .40), Sigma = tarcov)
cov(zhat2)

          [,1]       [,2]       [,3]
[1,] 37.311798 -5.2984514  1.7797147
[2,] -5.298451  1.0084439 -0.3467939
[3,]  1.779715 -0.3467939  0.2490788

• You can also specify a correlation matrix (1s on the diagonal of $\sum$ and covariances between -1 and 1)
• Often though, we may want to generate skewed data-- all our data so far have been normally distributed

To generate (univariate) skewed data, we can use Fleishman's (1978) Power Transformation

$$Y=a+bZ+c{Z}^2+d{Z}^3$$

$$Z\sim N(0,1)$$

• a, b, c, d are the coefficients needed to transform the unit normal variable to a non-normal variable. NOTE: a = -c

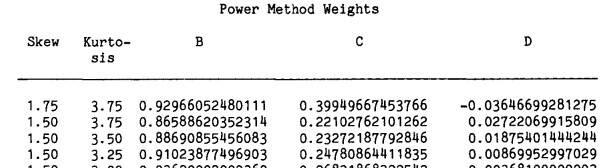
If we want a variable with a skewness of 1.75 and kurtosis of 3.75, get the coefficients from the table (p. 524)

Fleishman AI (1978). A Method for Simulating Non-normal Distributions. Psychometrika, 43, 521-532. doi: 10.1007/BF02293811

Example:

SKEWNESS  KURTOSIS      b      c       d
1.75      3.75          .9297  .3995   -.0365

set.seed(123)
Z <- rnorm(1000)
Y <- -.3995 + .9297 * Z + .3995 * Z^2 + -.0365 * Z^3
hist(Y)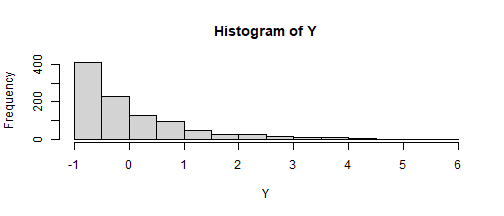

psych::skew(Y)

[1] 1.765537

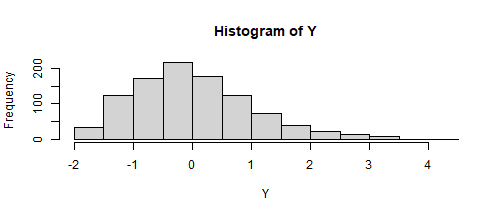
There is a table of coefficients in Fleishman's article: System of equations

SKEWNESS  KURTOSIS      b      c       d
1.75      3.75          .9297  .3995   -.0365

How do you get other coefficients?

library(SimMultiCorrData)
find_constants(method = "Fleishman", skews = 1.75, skurts = 3.75)

$constants
         c0          c1          c2          c3 
-0.39949647  0.92966020  0.39949647 -0.03646691 
$valid
[1] "FALSE"

• There are certain limits (boundaries) of the skewness and kurtosis that can be specified (cannot just specify any!). excess kurtosis $\ge$ skewness² - 2 (?) (skewness-kurtosis parabola)
• O. Astivia (U Washington) has written about this (video: https://www.youtube.com/watch?v=cYx0rRBW6qA&t=4947)
• Needs a large sample to stabilize

see https://search.r-project.org/CRAN/refmans/SimMultiCorrData/html/nonnormvar1.html

find_constants(method = "Fleishman", skews = 2, skurts = 10)

$constants
         c0          c1          c2          c3 
-0.20345030  0.63044307  0.20345030  0.09874172 
$valid
[1] "TRUE"

Z <- rnorm(10000)
Y <- -.20 + .63 * Z + .20 * Z^2 + .098 * Z^3
hist(Y)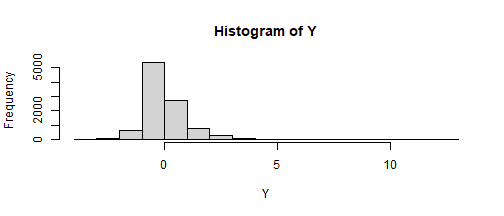

psych::skew(Y)

[1] 1.947779

update: Another way (not for multivariate data)-- just learned this while putting the slides together

coeff <- miceadds::fleishman_coef(mean = 0, sd = 1, skew = 2, kurt = 10)
print(coeff)

          a           b           c           d 
-0.20337308  0.63080518  0.20337308  0.09875006

X1 <- miceadds::fleishman_sim(N = 10000, coef = coeff)
#or... in one step...
X2 <- miceadds::fleishman_sim(N = 10000, mean = 0, sd = 1, skew = 2, kurt = 10)
par(mfrow = c(1, 2)) #for multipanel plot using base R
hist(X1)
hist(X2)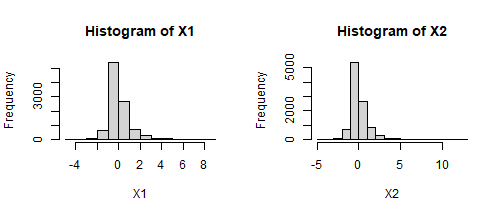

To generate multivariate, non-normal data, cannot just use the Fleishman transformation on its own

• IMPORTANT: We can't just use the same method!
• We can generate nonnormal, independent data, then transform
• However, the correlation/covariance structure will not be exactly the same as what we expect

To generate multivariate, non-normal data, cannot just use the Fleishman transformation on its own (need Vale & Maurelli's method)

• Need to create an "intermediate" correlation matrix, then that is what is factor analyzed to get the transformation matrix, then the generated data is then transformed using the usual Fleishman coefficients (so there is an extra step). Again, we can just use a function to simplify this:

set.seed(234); par(mfrow = c(1, 1)) #resetting to 1 plot
x2 <- mnonr::unonr(1000, c(1, 2), matrix(c(10, 2, 2, 5), 2, 2), 
                   skewness = c(-1, 2), kurtosis = c(3, 8))
psych::pairs.panels(x2)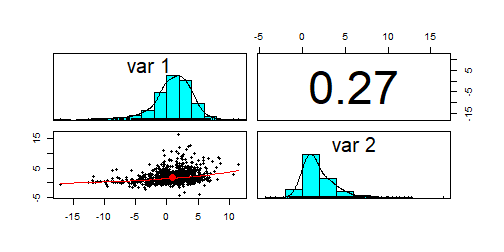

Vale, C. D. & Maurelli, V. A. (1983) Simulating multivariate non-normal distributions. Psychometrika, 48, 465-471.

Another way using the SimDesign package

library(SimDesign)
set.seed(122)
# univariate with skew
nonnormal <- rValeMaurelli(1000, 
  mean=10, sigma=5, skew=2, kurt=6)
hist(nonnormal)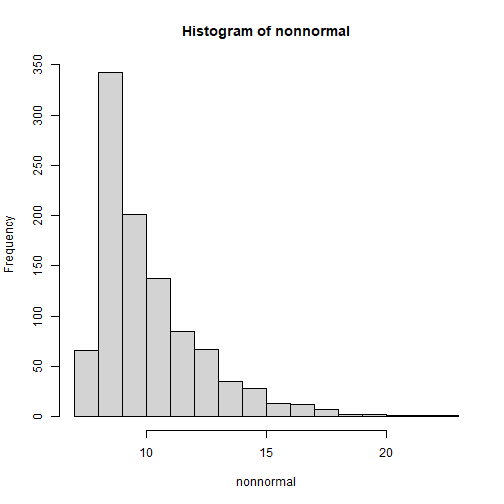

Another way using SimDesign package (cont.)

set.seed(123)
n <- 10000
r12 <- .4; r13 <- .9; r23 <- .1
cor <- matrix(c(1,r12,r13,
                r12,1,r23,
                r13,r23,1),3,3)
sk <- c(1.5,-1.5,0.5)
ku <- c(3.75,3.5,0.5)
nonnormal <- rValeMaurelli(n, 
 sigma = cor, skew = sk, 
 kurt = ku)
hist(nonnormal[,1])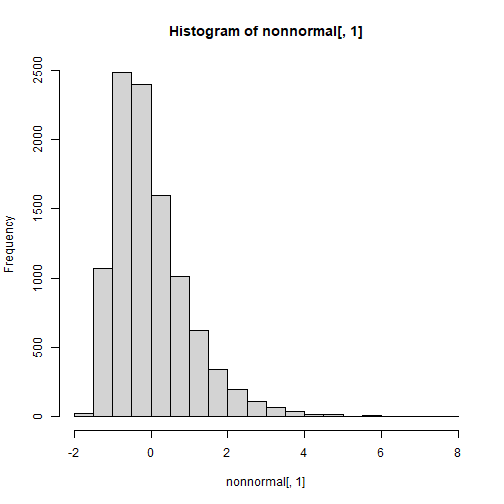

hist(nonnormal[,2])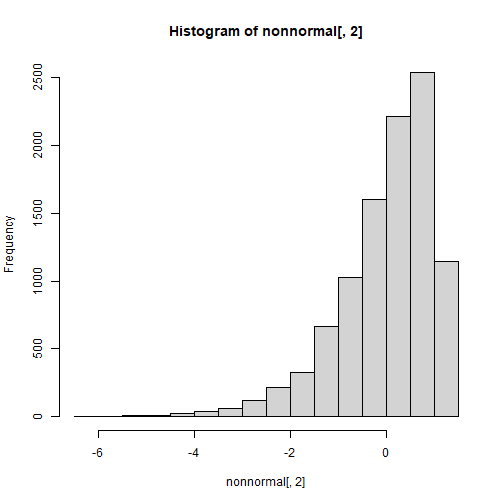

hist(nonnormal[,3])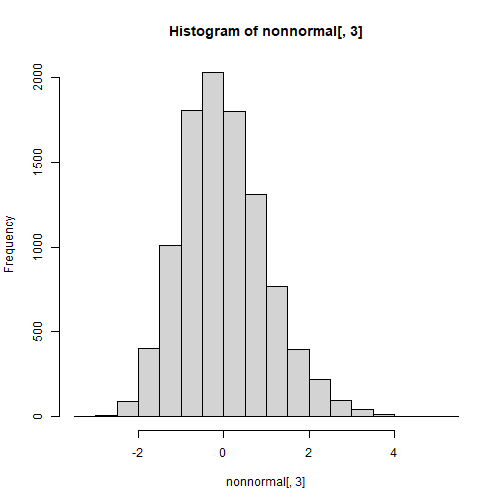

Sidenote: At times, the covariance is specified

... so need to just convert and the correlation is .28. This is just: $R=S^{-1}\Sigma S^{-1}$

mm <- matrix(c(10, 2, 2, 5), ncol = 2)
(sdm <- diag(sqrt(diag(mm)))) #diagonal matrix with sd on the diagonal

         [,1]     [,2]
[1,] 3.162278 0.000000
[2,] 0.000000 2.236068

Sinv <- solve(sdm)
Sinv %*% mm %*% Sinv #correlation matrix

          [,1]      [,2]
[1,] 1.0000000 0.2828427
[2,] 0.2828427 1.0000000

Or can simply use:

cov2cor(mm)

          [,1]      [,2]
[1,] 1.0000000 0.2828427
[2,] 0.2828427 1.0000000

There are several uses of this (generating multivariate correlated data)

• You can run regressions using a correlation/covariance matrix
• You can simulated CFA/SEM models too (w/c we haven't done)

e.g., a common factor model

Can be shown as:

$$\Sigma =\Lambda \Phi {\Lambda }^{\prime }+\Theta$$

where:

• $\Sigma$ = population correlation matrix (Sigma)
• $\Lambda$ = population factor loading matrix (Lambda)
• $\Phi$ = population factor correlation matrix (Phi)
• $\Theta$ = unique variances matrix (Theta)

Simulating a two factor model: Setting up the matrices...

Two factor model:

• The standardized loadings are .6 using two items each
• No cross loadings
• F1 and F2 are correlated at .5

Lam <- matrix(c(.6, 0,
                .6, 0,
                0, .6,
                0, .6), ncol = 2, byrow = T)
Phi <- matrix(c(1, .5,
                .5, 1), byrow = T, ncol = 2)
Theta <- diag(.64, 4)
cr <- Lam %*% Phi %*% t(Lam) + Theta
colnames(cr) <- rownames(cr) <- paste0("X", 1:4)
cr

     X1   X2   X3   X4
X1 1.00 0.36 0.18 0.18
X2 0.36 1.00 0.18 0.18
X3 0.18 0.18 1.00 0.36
X4 0.18 0.18 0.36 1.00

Estimate using lavaan... recovers what we specified (since we are working from the matrices)

library(lavaan)
mod <- '
  f1 =~ X1 + X2
  f2 =~ X3 + X4'
m1 <- cfa(model = mod, sample.cov = cr, sample.nobs = 1000 )
summary(m1, standardized = T)

Latent Variables:
                   Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
  f1 =~                                                                 
    X1                1.000                               0.600    0.600
    X2                1.000    0.164    6.101    0.000    0.600    0.600
  f2 =~                                                                 
    X3                1.000                               0.600    0.600
    X4                1.000    0.164    6.101    0.000    0.600    0.600
Covariances:
                   Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
  f1 ~~                                                                 
    f2                0.180    0.030    5.902    0.000    0.500    0.500
Variances:
                   Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
   .X1                0.639    0.065    9.818    0.000    0.639    0.640
   .X2                0.639    0.065    9.818    0.000    0.639    0.640
   .X3                0.639    0.065    9.818    0.000    0.639    0.640
   .X4                0.639    0.065    9.818    0.000    0.639    0.640

Can generate simulated data then using the matrices (using the methods we discussed)...

• Then you can evaluate the performance of your model
  • Examine fit indices?
  • Results of misspecification?
  • How does it deal with skewed data?
  • What about the use of different estimators?
  • What about ordinal data? (we haven't discussed that)

Others...

Another 'newish' package for generating simulated data is the faux (deBruine) package

• It looks interesting and has nice documentation

Others: generating categorical data with lavaan

library(lavaan)
# setup population model (from Sonja W)
# the x1 | -.6*t1 + .6*t2 specifies that x1 has two thresholds 
# (so three categories) set at -.6 and .6. lavaan uses delta 
# parameterization by default, so these thresholds
# cut up a standard normal distribution in 3 sections that map on to
# the observed categorical responses
popmod <- '
f1 =~ .8*x1 + .8*x2 + .8*x3 + .8*x4
x1 | -.6*t1 + .6*t2 + 1*t3
x2 | -.6*t1 + .6*t2 + 1*t3
x3 | -.6*t1 + .6*t2 + 1*t3
x4 | -.6*t1 + 0*t2 + .6*t3
'
simdat <- simulateData(model = popmod, 
 model.type = "cfa", std.lv = T,
 sample.nobs = 200)

added: 2023.08.30

psych::headTail(simdat)

     x1  x2  x3  x4
1     2   2   2   2
2     1   2   2   3
3     3   2   2   3
4     4   2   4   4
... ... ... ... ...
197   1   2   1   3
198   3   2   2   4
199   2   2   2   3
200   2   2   1   3

table(simdat$x1)

 1  2  3  4 
70 80 19 31

table(simdat$x4)

 1  2  3  4 
61 49 47 43